Master Multiplication And Division With “What Times What Equals”
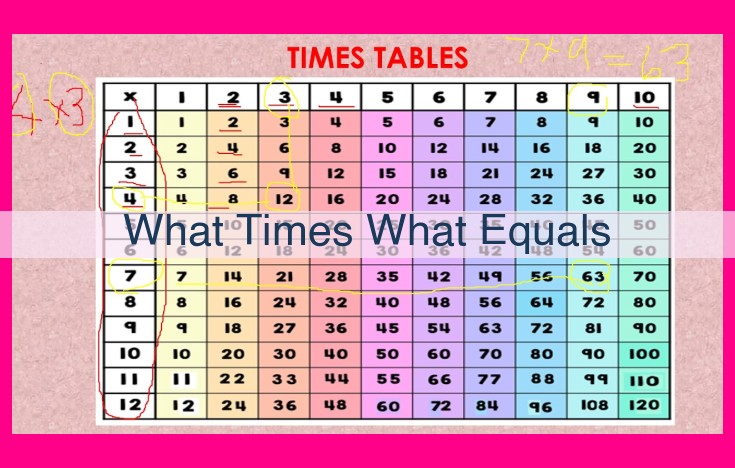
“What Times What Equals” explores the fundamental mathematical operations of multiplication and division, providing a comprehensive understanding of these crucial concepts. Through step-by-step explanations and practical examples, the book delves into the foundational mathematical concepts that underpin these operations, fostering a strong comprehension of the subject matter.
Mathematical Fundamentals: The Cornerstones of Math
Embark on a captivating journey into the realm of mathematics, where numbers and symbols dance together to unravel the intricacies of our world. As we delve into the mathematical fundamentals, we’ll unveil the building blocks that empower us to navigate the complexities of science, technology, and everyday life.
The Language of Arithmetic
Our mathematical expedition begins with the basic operations that lay the foundation for all subsequent mathematical endeavors: addition, subtraction, multiplication, division, and exponentiation. These operations allow us to combine, separate, increase, decrease, and manipulate numbers to solve real-world problems. Mastering these fundamental arithmetic skills is akin to unlocking the gateway to the world of quantitative reasoning.
Exploring Numbers: The Foundation of Mathematical Understanding
In the realm of mathematics, numbers serve as the fundamental building blocks, enabling us to quantify, measure, and describe the world around us. From the enigmatic zero to the boundless expanse of infinity, each type of number possesses unique characteristics and plays a crucial role in mathematical operations.
Zero: The Enigmatic Foundation
Zero, the enigmatic placeholder, marks the absence of quantity. Its introduction revolutionized mathematics, allowing for the concept of nothingness and enabling operations like subtraction. Zero acts as a neutral element in arithmetic, neither increasing nor decreasing the value of other numbers it accompanies.
One: The Cornerstone of Counting
From a single object to countless stars, the concept of one is pivotal in understanding numbers. It serves as the basis for counting, establishing the foundation for all mathematical operations. By repeatedly adding one, we can build larger numbers and explore the vastness of the number system.
Negative Numbers: Expanding the Horizon
Negative numbers extend the numerical realm beyond zero, delving into values less than nothing. They represent quantities that are opposite in direction or nature to positive numbers. Negative numbers find applications in everyday scenarios, such as expressing temperatures below freezing or financial deficits.
Rational Numbers: Fractions and Decimals
Rational numbers, including fractions and decimals, represent numbers that can be expressed as a quotient of two integers. Fractions denote parts of a whole, while decimals offer a convenient way to represent non-integer values. Rational numbers are essential for precise measurements and calculations in various fields.
Irrational Numbers: Unveiling the Non-Terminating and Non-Repeating
Irrational numbers, such as pi and the square root of 2, cannot be expressed as a simple fraction. Their decimal representations continue indefinitely without any repeating pattern. Irrational numbers are often encountered in geometry, trigonometry, and natural phenomena.
Embarking on this mathematical journey through numbers unveils a world of wonder and complexity. From the enigmatic zero to the boundless infinity, each type of number holds its significance, enriching our understanding of the universe and empowering us to solve problems and make informed decisions.
Algebraic Concepts: Unveiling the Language of Mathematics
Algebra, a fascinating realm of mathematics, unveils a powerful language that empowers us to express and solve complex problems. It introduces concepts that unlock the secrets of the unknown and empowers us to make sense of the intricate patterns that govern our world.
At the heart of algebraic expressions lie terms, the building blocks that combine to construct mathematical statements. Each term comprises a coefficient, a numerical multiplier, and a variable, a placeholder for unknown values. Coefficients scale the variable’s impact on the expression, while variables represent the unknown quantities that we seek to solve for.
Through algebraic manipulation, we simplify these expressions, revealing their underlying structure. Equations, mathematical statements that declare equality between two expressions, take center stage in algebra’s problem-solving toolkit. They challenge us to unveil the unknown values hidden within, employing various solution techniques that range from simple substitution to complex mathematical procedures.
Algebra empowers us to unravel the mysteries of the unknown, explore the relationships between variables, and make predictions based on mathematical patterns. It is a language that transcends boundaries, connecting us to the fundamental principles that govern our universe and empowering us to unlock its secrets.